![]()
Have you ever walk into a job interview, and were asked to design a program to find if 2 rectangles intersect with each other or not?
This apparently is a common “technical” question in a job interview. I do agree that it is an interesting question to evaluate your analysis skill together with some emphasis on your coding skill, the coding part is not complicated at all. Giving all the add-on packages available nowadays in the different programming languages, I wouldn’t be surprised if you will find the right library with a rectangle intersect function, that all you have to do is call it with the 2 rectangles as input.
But anyway, the fun is with the analysis of the problem at hand and how to implement it in your language of choice.
I’m going to do this case study here using the core Java language without any add-on packages. Rectangle can be define a number of ways, in this example, we will define rectangle with 2 points, the lower left corner (x1, y1) and the upper right corner (x2, y2). Helper methods are also created to find the rectangle’s width, height, and area.
/*
* A rectangle is defined by 2 points
* x1, y1 represent the lower left corner point
* x2, y2 represent the upper right corner point
*/
public Rect (int x1, int y1, int x2, int y2) {
this.x1 = x1;
this.y1 = y1;
this.x2 = x2;
this.y2 = y2;
}
public int width() {
return x2 - x1;
}
public int height() {
return y2 - y1;
}
// area of a rectangle is width * height
public int area() {
return (this.width() * this.height());
}
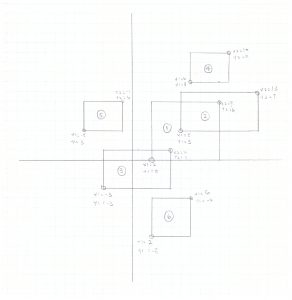
To start with, I layout a few rectangles on a piece of paper so that I can do my analysis, sorry, it is done with pencil and graph paper, not very attractive, will update later with better graphic I hope. (Hint: click on image to enlarge it)
// Let's create a few rectangles Rect r1 = new Rect (2,0,9,6); Rect r2 = new Rect (5,3,13,7); Rect r3 = new Rect (-3,-3,4,1); Rect r4 = new Rect (6,8,10,11); Rect r5 = new Rect (-5,3,-1,6); Rect r6 = new Rect (2,-8,6,-4);
There are 6 rectangles, some of them intersect, some of them don’t.
This is method 1 in my implementation:
After observing the intersection between 2 rectangles, I was able to come up with this formula to calculate the actual intersection area.
// Find the intersection area between 2 rectangle
// and return the intersection rectangle
public Rect intersection(Rect r) {
Rect result = new Rect ( (this.x1 > r.x1) ? this.x1 : r.x1,
(this.y1 > r.y1) ? this.y1 : r.y1,
(this.x2 < r.x2) ? this.x2 : r.x2,
(this.y2 < r.y2) ? this.y2 : r.y2 );
// to be a valid rectangle x1 can not be greater than x2
// and y1 can not be greater than y2.
if (result.x1 > result.x2) { result.x1 = result.x2 = 0; }
if (result.y1 > result.y2) { result.y1 = result.y2 = 0; }
return result;
}
Once we have the intersection, if the area of the intersection is greater than 0, the 2 rectangles intersect. If the area is 0 or less than 0, the 2 rectangles do not intersect.
// case study 1: find the intersection area between the 2 rectangles
// the 2 rectangle intersect if result is a valid rectangle,
// meaning it's area > 0,
public boolean intersect1(Rect r) {
// Method1 : First find the intersection
// if area of the intersection is greater than 0, they intersect.
Rect i = this.intersection(r);
return i.area() > 0;
}
This is pretty cool so far, but I feel that this is a bit more complicated to my liking.
This is method 2 of my implementation:
I analyse a bit further, and think that it is actually easier to determine if the 2 rectangles DO NOT intersect. Based on the simple evaluation of the Xs and Ys, it can be easily confirmed that the 2 rectangles DO NOT intersect.
// case study 2: we can also find out when the rectangles do NOT intersect by
// the following logic:
// if the lower left point of R1 is
// greater than the upper right point of R2
// or
// if the lower left point of R2 is
// greater than the upper right point of R1
// and just return the negative value to indicate if it intersect or vice versa.
public boolean intersect2(Rect r) {
return !(this.x1 > r.x2 || this.y1 > r.y2 || r.x1 > this.x2 || r.y1 > this.y2);
}
I do feel that this second solution is very simple and elegant. The only drawback is that it will not tell you what the actual intersection area is, so if you actually need to know the intersection area, method 1 is still preferred.
Test cases:
I created a number of test cases and compare results from the 2 methods, they produced same and consistent results. Here is the code for one of the test and the result from all 9 test cases.
System.out.println ("\n--- Test Case 1 ---");
System.out.println ("r2 = " + r2);
System.out.println ("r3 = " + r3);
System.out.println ("r2 intersection r3 = " + r2.intersection(r3));
System.out.println ("r2 intersect1 r3? " + r2.intersect1(r3));
System.out.println ("r2 intersect2 r3? " + r2.intersect2(r3));
In case if you are interested, the full source code is in my Github repository.
Hope you enjoy this case study analysis, happy coding !