Math puzzle 2 – answer

Ok, let’s do some analysis and deduction here. Let’s look at the facts provide to us.

Fact #1: with the coins, the cashier can not provide change in coins, a dollar, half dollar, quarter, dime, or nickel.

Let’s simplify the situation by figure out what’s NOT possible.

• She can not change for a dollar, meaning that she could not have more than one half dollar
• She can not change for a half dollar, meaning that she could not have more than one quarter, and no more than 4 dimes
• She can not change for a dime, meaning that she could not have more than 1 nickel
• She can not change for a nickel, meaning that she could not have more than 4 pennies

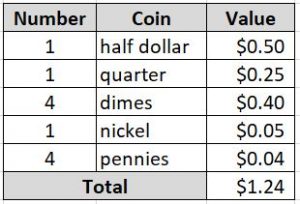
Base on the deduction above, here are what she may have in her cash register:

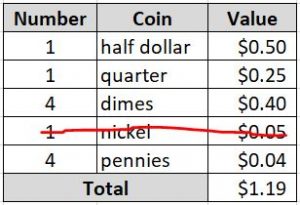
We should also observe that with these coins, she can still change for a dollar with a half dollar, a quarter, 2 dimes, and a nickel. She can also change for a quarter with 2 dimes, and 1 nickel.  This means that we need to eliminate the nickel as well.

Now we can safely say that with these coins in the cash register, she can not provide any change in coin.

Fact #2: the cashier has exactly $1.15 in coins

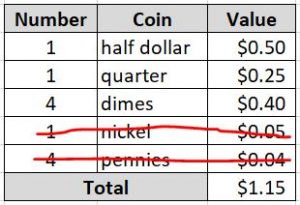
So base on our analysis and deduction with fact #1, we have a total of $1.19 in coins in the cash register, that is not right, it is 4 cents more that what she has.  So the only way to make up 4 cents is 4 pennies, we can now eliminate that as well.

Bingo, I think we have it.  Now we can confirm a total to $1.15 in coins in the cash register but she still can not provide change for a dollar, half dollar, quarter, dime, or nickel.

This may not be a really difficult exercise, but it is kind of interesting because it is a very good example on how to leverage simple facts to create your deduction to get to the solution.  This type of challenges happen all around us in real life, use your brain wisely and you will be able to overcome the challenges.

Here is a link to the original post for this puzzle in case if you want to see it again.